O problema pode ser resolvido em O (polylog (b)).
Definimos f(d, n)como o número de inteiros de até d dígitos decimais com soma de dígitos menor ou igual a n. Pode-se ver que essa função é dada pela fórmula

Vamos derivar essa função, começando com algo mais simples.
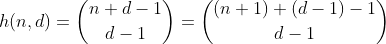
A função h conta o número de maneiras de escolher elementos d - 1 de um conjunto múltiplo contendo n + 1 elementos diferentes. É também o número de maneiras de particionar n em compartimentos d, o que pode ser facilmente visto construindo cercas d-1 em torno de n e somando cada seção separada. Exemplo para n = 2, d = 3 ':
3-choose-2 fences number
-----------------------------------
11 ||11 002
12 |1|1 011
13 |11| 020
22 1||1 101
23 1|1| 110
33 11|| 200
Portanto, h conta todos os números com uma soma de dígitos de n e d dígitos. Exceto que ele só funciona para n menos de 10, pois os dígitos são limitados de 0 a 9. Para corrigir isso para os valores de 10 a 19, precisamos subtrair o número de partições com um compartimento com um número maior que 9, que chamarei de compartimentos transbordados a partir de agora.
Este termo pode ser calculado reutilizando h da seguinte maneira. Contamos o número de maneiras de particionar n - 10 e, em seguida, escolhemos um dos compartimentos para colocar os 10, o que resulta no número de partições com um compartimento transbordado. O resultado é a seguinte função preliminar.
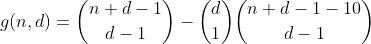
Continuamos dessa maneira por n menor ou igual a 29, contando todas as maneiras de particionar n - 20 e, em seguida, escolhendo 2 posições onde colocamos os 10's, contando assim o número de partições contendo 2 posições excedentes.
Mas, neste ponto, temos que ter cuidado, porque já contamos as partições com 2 posições transbordadas no termo anterior. Não só isso, mas na verdade contamos duas vezes. Vamos usar um exemplo e examinar a partição (10,0,11) com a soma 21. No termo anterior, subtraímos 10, calculamos todas as partições dos 11 restantes e colocamos os 10 em um dos 3 compartimentos. Mas essa partição específica pode ser alcançada de duas maneiras:
(10, 0, 1) => (10, 0, 11)
(0, 0, 11) => (10, 0, 11)
Como também contamos essas partições uma vez no primeiro termo, a contagem total de partições com 2 compartimentos excedidos é de 1 - 2 = -1, portanto, precisamos contá-las mais uma vez adicionando o próximo termo.
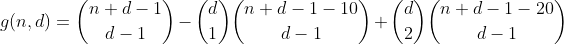
Pensando um pouco mais sobre isso, descobrimos em breve que o número de vezes que uma partição com um número específico de posições transbordadas é contada em um termo específico pode ser expressa pela tabela a seguir (a coluna i representa o termo i, partições de linha j com j transbordada caixas).
1 0 0 0 0 0 . .
1 1 0 0 0 0 . .
1 2 1 0 0 0 . .
1 4 6 4 1 0 . .
. . . . . .
. . . . . .
Sim, é o triângulo Pascal. A única contagem em que estamos interessados é a da primeira linha / coluna, ou seja, o número de partições com zero compartimentos excedidos. E como a soma alternada de cada linha, exceto a primeira, é igual a 0 (por exemplo, 1 - 4 + 6 - 4 + 1 = 0), é assim que nos livramos deles e chegamos à penúltima fórmula.
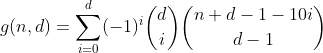
Esta função conta todos os números com dígitos d com uma soma de dígitos de n.
Agora, e os números com soma de dígitos menor que n? Podemos usar uma recorrência padrão para binômios mais um argumento indutivo, para mostrar que
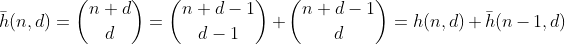
conta o número de partições com soma de dígitos no máximo n. E disso f pode ser derivado usando os mesmos argumentos que para g.
Usando esta fórmula, podemos, por exemplo, encontrar o número de números pesados no intervalo de 8000 a 8999 1000 - f(3, 20), pois , porque existem milhares de números nesse intervalo, e temos que subtrair o número de números com soma de dígitos menor ou igual a 28 enquanto deduz que o primeiro dígito já contribui com 8 para a soma do dígito.
Como um exemplo mais complexo, vejamos o número de números pesados no intervalo 1234..5678. Podemos primeiro ir de 1234 a 1240 nas etapas de 1. Em seguida, vamos de 1240 a 1300 nas etapas de 10. A fórmula acima nos fornece o número de números pesados em cada intervalo:
1240..1249: 10 - f(1, 28 - (1+2+4))
1250..1259: 10 - f(1, 28 - (1+2+5))
1260..1269: 10 - f(1, 28 - (1+2+6))
1270..1279: 10 - f(1, 28 - (1+2+7))
1280..1289: 10 - f(1, 28 - (1+2+8))
1290..1299: 10 - f(1, 28 - (1+2+9))
Agora vamos de 1300 a 2000 em etapas de 100:
1300..1399: 100 - f(2, 28 - (1+3))
1400..1499: 100 - f(2, 28 - (1+4))
1500..1599: 100 - f(2, 28 - (1+5))
1600..1699: 100 - f(2, 28 - (1+6))
1700..1799: 100 - f(2, 28 - (1+7))
1800..1899: 100 - f(2, 28 - (1+8))
1900..1999: 100 - f(2, 28 - (1+9))
De 2000 a 5000 em etapas de 1000:
2000..2999: 1000 - f(3, 28 - 2)
3000..3999: 1000 - f(3, 28 - 3)
4000..4999: 1000 - f(3, 28 - 4)
Agora temos que reduzir o tamanho da etapa novamente, passando de 5000 para 5600 nas etapas de 100, de 5600 para 5670 nas etapas de 10 e, finalmente, de 5670 para 5678 nas etapas de 1.
Um exemplo de implementação do Python (que recebeu algumas otimizações e testes enquanto isso):
def binomial(n, k):
if k < 0 or k > n:
return 0
result = 1
for i in range(k):
result *= n - i
result //= i + 1
return result
binomial_lut = [
[1],
[1, -1],
[1, -2, 1],
[1, -3, 3, -1],
[1, -4, 6, -4, 1],
[1, -5, 10, -10, 5, -1],
[1, -6, 15, -20, 15, -6, 1],
[1, -7, 21, -35, 35, -21, 7, -1],
[1, -8, 28, -56, 70, -56, 28, -8, 1],
[1, -9, 36, -84, 126, -126, 84, -36, 9, -1]]
def f(d, n):
return sum(binomial_lut[d][i] * binomial(n + d - 10*i, d)
for i in range(d + 1))
def digits(i):
d = map(int, str(i))
d.reverse()
return d
def heavy(a, b):
b += 1
a_digits = digits(a)
b_digits = digits(b)
a_digits = a_digits + [0] * (len(b_digits) - len(a_digits))
max_digits = next(i for i in range(len(a_digits) - 1, -1, -1)
if a_digits[i] != b_digits[i])
a_digits = digits(a)
count = 0
digit = 0
while digit < max_digits:
while a_digits[digit] == 0:
digit += 1
inc = 10 ** digit
for i in range(10 - a_digits[digit]):
if a + inc > b:
break
count += inc - f(digit, 7 * len(a_digits) - sum(a_digits))
a += inc
a_digits = digits(a)
while a < b:
while digit and a_digits[digit] == b_digits[digit]:
digit -= 1
inc = 10 ** digit
for i in range(b_digits[digit] - a_digits[digit]):
count += inc - f(digit, 7 * len(a_digits) - sum(a_digits))
a += inc
a_digits = digits(a)
return count
Editar : substituiu o código por uma versão otimizada (que parece ainda mais feia que o código original). Também consertei alguns casos de canto enquanto eu estava nisso. heavy(1234, 100000000)leva cerca de um milissegundo na minha máquina.
