A etapa "dividir" em uma ordem de mesclagem pode ser evitada?

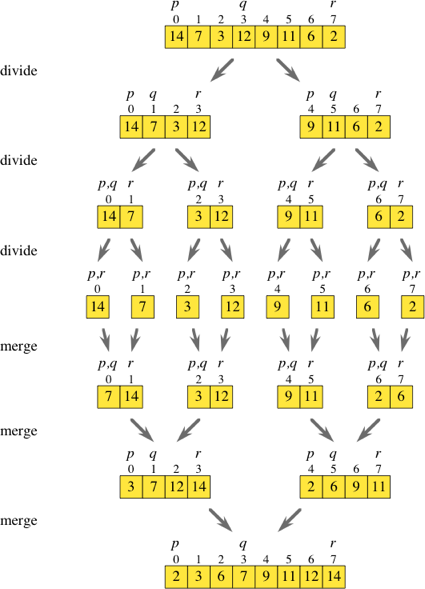
Mesclar classificação

Portanto, a classificação por mesclagem é um algoritmo de divisão e conquista. Enquanto eu observava o diagrama acima, estava pensando se era possível ignorar basicamente todas as etapas de divisão.

Se você iterou sobre a matriz original enquanto pulava duas vezes, poderia obter os elementos no índice iei + 1 e colocá-los em suas próprias matrizes ordenadas. Depois de ter todas essas sub-matrizes ([7,14], [3,12], [9,11] e [2,6], como mostrado no diagrama), você pode simplesmente prosseguir com a rotina de mesclagem normal para obter uma matriz classificada.

A iteração na matriz e a geração imediata das sub-matrizes necessárias são menos eficientes do que as etapas de divisão na sua totalidade?

— Jimmy_Rustle
fonte

Veja também: cs.stackexchange.com/questions/77075/…

— Omar

Respostas:

A confusão surge da diferença entre a descrição conceitual do algoritmo e sua implementação .

A classificação de mesclagem lógica é descrita como dividir a matriz em matrizes menores e depois mesclá-las novamente. No entanto, "dividir a matriz" não implica "criar uma matriz inteiramente nova na memória" ou algo assim - poderia ser implementado no código como

/*
 * Note: array is now split into  [0..n) and [n..N)
 */

isto é, nenhum trabalho real ocorre e a "divisão" é puramente conceitual. Portanto, o que você sugere certamente funciona, mas logicamente você ainda está "dividindo" as matrizes - você não precisa de nenhum trabalho do computador para fazê-lo :-)

— psmears
fonte

Pessoalmente, gosto muito da classificação de mesclagem de baixo para cima, porque é mais simples de implementar de uma maneira que permite evitar a alocação de um buffer temporário em cada nível de recursão. Em vez disso, você aloca um buffer uma vez e faz ping-pong entre eles.

— ratchet freak -

Essa divisão - computacionalmente é uma opção não operacional ... mais os OPs é apenas uma introdução de um equivalente a uma fusão de matrizes de elemento único e começar a usar a mesclagem a partir da 2ª etapa, o que parece redundante, porque a mesclagem original também funciona. Não faz sentido otimizar isso. Ele apenas introduz conceitos e lógica redundantes.

— Luk32

@ratchetfreak: Eu também adoro, mas, infelizmente, não é equivalente a top-down (pelo menos a versão que eu conheço). Ele fará a fusão de maneira diferente, basicamente arredondando para o próximo comprimento de matriz de potência de 2, que eu acho que pode até ser um pouco mais lento. Você conhece uma versão de baixo para cima que faz exatamente a mesma fusão sem pagar um alto custo em outro lugar?

— user541686

@Mehrdad, o único problema real é a pequena cauda que precisa ser mesclada. Na pior das hipóteses, isso significa que outro passe será mesclado em um único item para arrays de comprimento 1<<n+1. Embora eu tenha certeza de que você pode ajustar as coisas para que uma cauda muito pequena seja mesclada em um passe mais baixo.

— ratchet freak

@psmears "você simplesmente não precisa de nenhum trabalho do computador para fazer isso" - então estou supondo que o custo de desempenho de n chamadas de alguma função de divisão recursiva (7 chamadas no diagrama de exemplo) seja basicamente insignificante?

— Jimmy_Rustle

Eu acho que você quer dizer com implementação de baixo para cima . Na implementação de baixo para cima, você inicia com elementos de célula única e move-se para cima, mesclando elementos em listas / matrizes maiores. Basta inverter as setas da figura acima, começando na matriz do meio, ou seja, matrizes de um elemento.

Além disso, convém otimizar a classificação de mesclagem dividindo matrizes até que elas atinjam um tamanho constante, após o qual você simplesmente as classifica usando, por exemplo, classificação de inserção.

Caso contrário, a classificação sem dividir a matriz não é possível. De fato, a essência da classificação Merge é dividir e classificar os sub-arranjos, isto é, dividir e conquistar.

— fade2black
fonte