Polígonos separados com base na interseção usando PostGIS

Eu tenho uma tabela PostGIS de polígonos, onde alguns se cruzam. Isto é o que estou tentando fazer:

• Para um determinado polígono selecionado por id, forneça todos os polígonos que se cruzam. Basicamente,select the_geom from the_table where ST_Intersects(the_geom, (select the_geom from the_table where source_id = '123'))
• A partir desses polígonos, preciso criar novos polígonos para que a interseção se torne um novo polígono. Portanto, se o polígono A cruzar com o polígono B, receberei 3 novos polígonos: A menos AB, AB e B menos AB.

Alguma ideia?

Como você disse que obtém um grupo de polígonos que se cruzam para cada polígono em que está interessado, convém criar o que é chamado de "sobreposição de polígono".

Não é exatamente isso que a solução de Adam está fazendo. Para ver a diferença, dê uma olhada nesta foto de um cruzamento ABC:

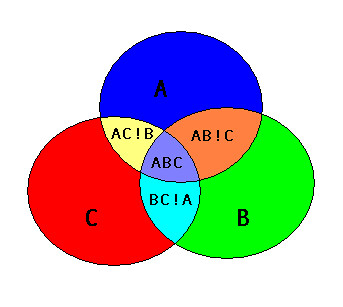
Acredito que a solução de Adam criará um polígono "AB" que cubra a área de "AB! C" e "ABC", bem como um polígono "AC" que cubra "AC! B" e "ABC" e um " BC "polígono que é" BC! A "e" ABC ". Portanto, os polígonos de saída "AB", "AC" e "BC" se sobrepõem à área "ABC".

Uma sobreposição de polígono produz polígonos sem sobreposição, portanto AB! C seria um polígono e ABC seria um polígono.

Criar uma sobreposição de polígono no PostGIS é realmente bastante simples.

Existem basicamente três etapas.

O passo 1 é extrair o trabalho de linha [Observe que estou usando o anel externo do polígono, fica um pouco mais complicado se você quiser manipular corretamente os orifícios]:

SELECT ST_ExteriorRing(polygon_col) AS the_geom FROM my_table) AS lines

O passo 2 é "nodo" o trabalho de linha (produza um nó em cada interseção). Algumas bibliotecas como o JTS têm classes "Noder" que você pode usar para fazer isso, mas no PostGIS a função ST_Union faz isso por você:

SELECT ST_Union(the_geom) AS the_geom FROM (...your lines...) AS noded_lines

A etapa 3 é criar todos os possíveis polígonos não sobrepostos que podem vir de todas essas linhas, executados pela função ST_Polygonize :

SELECT ST_Polygonize(the_geom) AS the_geom FROM (...your noded lines...)

Você pode salvar a saída de cada uma dessas etapas em uma tabela temporária ou combiná-las em uma única instrução:

CREATE TABLE my_poly_overlay AS
SELECT geom FROM ST_Dump((
    SELECT ST_Polygonize(the_geom) AS the_geom FROM (
        SELECT ST_Union(the_geom) AS the_geom FROM (
            SELECT ST_ExteriorRing(polygon_col) AS the_geom FROM my_table) AS lines
        ) AS noded_lines
    )
)

Estou usando ST_Dump porque a saída de ST_Polygonize é uma coleção de geometria e (geralmente) é mais conveniente ter uma tabela em que cada linha é um dos polígonos que compõem a sobreposição de polígonos.

Se bem entendi, você quer pegar (A é a geometria esquerda, B é a direita):

Imagem de A∪B http://img838.imageshack.us/img838/3996/intersectab1.png

E extrair:

A ∖ AB

Imagem de A ∖ AB http://img830.imageshack.us/img830/273/intersectab2.png

AB

Imagem da AB http://img828.imageshack.us/img828/7413/intersectab3.png

e B ∖ AB

Imagem de B ∖ AB http://img839.imageshack.us/img839/5458/intersectab4.png

Ou seja - três geometrias diferentes para cada par que se cruza.

Primeiro, vamos criar uma visualização de todas as geometrias que se cruzam. Supondo que o nome da sua tabela seja polygons_table, usaremos:

CREATE OR REPLACE VIEW p_intersections AS    -- Create a view with the 
SELECT t1.the_geom as t1_geom,               -- intersecting geoms. Each pair
       t2.the_geom as t2_geom                -- appears once (t2.id<t2.id)
    FROM polygons_table t1, polygons_table t2  
         WHERE t1.id<t2.id AND t1.the_geom && t2.the_geom 
                           AND intersects t1.the_geom, t2.the_geom;

Agora temos uma visão (praticamente uma tabela somente leitura) que armazena pares de geoms que se cruzam, onde cada par aparece apenas uma vez devido à t1.id<t2.idcondição.

Agora vamos reunir suas interseções - A∖AB, ABe B∖AB, usando SQL UNIONnas três consultas:

--AB:
SELECT ST_intersection(t1.the_geom, t2.the_geom) 
    AS geom 
    FROM p_intersections

UNION 

--A∖AB:
SELECT ST_Difference(t1.the_geom, t2.the_geom) 
    AS geom 
    FROM p_intersections

UNION

--B∖AB:
SELECT ST_Difference(t2.the_geom, t1.the_geom) 
    AS geom 
    FROM p_intersections;

Notas:

1. O &&operador é usado como um filtro antes do intersectsoperador, para melhorar o desempenho.
2. Eu escolhi criar uma VIEWconsulta gigantesca em vez de uma; Isto é apenas por conveniência.
3. Se você quis dizer ABé a união, não a interseção, de Ae B- Use ST_Union em vez de st_intersection na UNIONconsulta nos locais apropriados.
4. O ∖sinal é um sinal unicode para Definir diferença; remova-o do código, se confundir seu banco de dados.
5. Imagens cortesia da categoria de teoria dos conjuntos do Wikimedia Commons .

O que você está descrevendo é a maneira como o operador Union trabalha no ArcGIS, mas é um pouco diferente de Union ou Intersection no mundo GEOS. O manual Shapely tem exemplos de como os conjuntos funcionam no GEOS . No entanto, o wiki do PostGIS tem um bom exemplo de trabalho de linha, o que deve fazer o truque para você.

Como alternativa, você pode calcular três coisas:

1. ST_Intersection (geom_a, geom_b)
2. ST_Diferença (geom_a, geom_b)
3. ST_Diferença (geom_b, geom_a)

Esses devem ser os três polígonos que você mencionou no seu segundo marcador.

Algo como:

INSERIR EM new_table VALUES ((selecione id, the_geom da tabela_ antiga onde st_intersects (the_geom, (selecione the_geom da tabela_ antiga onde id = '123')) = true

EDIT: você precisa da interseção real do polígono.

INSERT INTO new_table values ​​((selecione id, ST_Intersection (the_geom, (selecione the_geom da antiga onde id = 123))

veja se isso funciona.