Por que a distância de foco na qual minha lente possui ampliação 1 corresponde à fórmula?

Na página da Wikipedia sobre ampliação , tenho a seguinte igualdade:

M = d _i / d _o = f / (d _o - f) = (d _i - f) / f

H com a ampliação, f o comprimento focal, d _o a distância do objecto para a lente, e d _i a distância entre a lente para o sensor.

Portanto, quando a ampliação é 1, deveríamos ter _di = d _o = 2f.

Com minha lente macro (EF 100mm f / 2.8 L IS USM Macro), a distância mínima de trabalho (do sujeito ao sensor) é de 30 cm, a essa distância a ampliação é 1. Pelo que eu não entendo da fórmula, essa distância deve ser d _i + d _o = 4-F = 40 centímetros.

Então, acho que estou perdendo alguma coisa, alguém pode explicar onde estou errado?

A equação assume uma lente simples de elemento único que é bilateralmente simétrica. A lente da câmera, para mitigar as 7 principais aberrações (deficiências que se degradam), é construída usando vários elementos individuais da lente de vidro. Alguns são positivos em poder, outros com poder negativo. Alguns são espaçados pelo ar e outros são cimentados. Como essa matriz se torna bastante complexa, o ponto a partir do qual medimos a distância focal provavelmente será desviado do centro físico do barril da lente.

Em um verdadeiro design de telefoto, o nodal traseiro (ponto de medição) é deslocado para frente. Essa ação reduz o comprimento do barril da lente, tornando a câmera e a lente menos difíceis de segurar, usar e armazenar. Em alguns modelos, o nodal traseiro pode cair no ar à frente do barril da lente.

Conforme a equação afirma: na unidade (ampliação 1), a distância do assunto é de 2 comprimentos de distância focal para a frente e o foco traseiro é de 2 comprimentos de foco atrás do nodal traseiro. O problema é --- você não pode localizar facilmente o nodal traseiro. No entanto, uma vez alcançada a ampliação 1, agora você pode medir a distância entre o objeto e a imagem. Muitas câmeras fornecem um símbolo (círculo dividido por uma linha) no quadro da câmera; para localizar a posição do plano da imagem.

De qualquer forma, meça a distância entre a imagem e a imagem e divida por 4. Essa divisão revela a distância focal. Divida por 2 e esta divisão localiza o ponto nodal traseiro. Agora você está melhor equipado para utilizar a "fórmula do fabricante de lentes".

Antes de tudo, parabéns pelo seu esforço para dividir um problema de fotografia nos primeiros princípios.

A discrepância que você observou decorre de uma simplificação excessiva comum. Sua lente de 100 mm é na verdade o que os engenheiros ópticos chamam de "conjunto de lentes". Como você provavelmente sabe, ela é composta por vários elementos de lentes em grupos que trabalham em conjunto para formar, refinar e transmitir a imagem vista pelo seu sensor de imagem.

Se o seu conjunto de lentes de 100 mm consistisse em um único elemento de lente de 100 mm, você teria distorções maciças e apenas vermelho, verde ou azul poderiam estar em foco por vez, mas a equação de ampliação da lente fina que você vinculou seria verdadeira. A ampliação de 1 seria alcançada quando o sujeito estivesse a 200 mm do ponto nodal e o conjunto da lente precisaria ser fisicamente maior que 200 mm de comprimento. Mesmo assim, isso seria estritamente preciso na medida em que a equação da lente fina for apropriada (e não é particularmente apropriada aqui.) Uma resposta adequada viria de uma derivação da equação do criador de lentes

Um corolário da diferença entre uma montagem e uma lente fina são pontos nodais bilocados. Uma lente fina possui um único local para os pontos nodais dianteiro e traseiro; Ambos são colocados com o aluno de entrada. Se isso fosse verdade no seu conjunto de lentes, você seria capaz de liberar as lentesgirando em torno da abertura da lente sem paralaxe ao objeto ou sensor. Tenho certeza que se você tentasse isso com a macro de 100 mm, descobriria que isso não é verdade. Uma lente espessa possui dois pontos nodais que são colocados apenas se seu índice líquido for 0, ou seja, não possui distância focal. Um conjunto de lente pode ser aproximado por uma lente virtual espessa com dois índices idealizados, de modo que a lente virtual tenha os mesmos vértices, distâncias focais relativas, pupila de entrada e pontos nodais (de forma destacada) do conjunto da lente.

Para obter crédito extra, você pode verificar a descrição de uma lente composta e tentar adivinhar quais combinações de distâncias focais da lente criariam a situação que você descreveu. NB a "ampliação do telescópio". Isso é essencialmente o que um designer de lentes faz.

Para uma leitura adicional, você pode conferir os diferentes tipos de designs de lentes fotográficas

A maioria das lentes da distância focal fixa fixa alterando a distância focal, além de mover o (s) ponto (s) nodal (s) da lente. Para focar em um objeto próximo à câmera, a lente reduz sua distância focal. Uma lente especificada como "100 mm" geralmente é "100 mm quando focada no infinito", mas não necessariamente quando focada em um objeto próximo.

Há duas razões pelas quais a distância do objeto à imagem não é de 40 cm na ampliação da unidade:

1. a distância focal da lente não pode ser 100 mm
2. a distância entre os planos principais pode não ser zero.

Qual destas razões é a mais importante é impossível dizer sem informações detalhadas sobre o design óptico da lente.

Comprimento focal

O valor “100 mm” escrito na própria lente é uma distância focal nominal , que normalmente é um valor arredondado da distância focal real quando a lente é focada no infinito.

Algumas lentes, geralmente chamadas de lentes de "foco da unidade", conseguem foco movendo o conjunto óptico como um todo. Essas lentes têm uma distância focal que não varia com o foco. No entanto, muitas lentes complexas, incluindo praticamente qualquer lente macro moderna, têm algum tipo de "correção de curto alcance" (na linguagem da Nikon): sua fórmula óptica muda conforme o foco, o que permite uma melhor correção de aberrações. Essas lentes têm uma distância focal que varia conforme o foco.

Esses dois fatos: o arredondamento da distância focal nominal e o fato de variar quando você foca significa que você não sabe qual é a distância focal real da lente na ampliação da unidade.

Aviões principais

A página da Wikipedia que você menciona define d _o e _di como a distância da lente ao objeto (resp. Image), mas observe que essas definições aparecem em uma seção especificamente sobre lentes finas . Como sua lente é uma lente composta espessa, isso levanta a questão da aplicabilidade da fórmula.

Acontece que a aproximação de lente fina não é aplicável nessa situação. No entanto, a fórmula ainda é válida se interpretada no contexto do modelo de lente espessa . Nesse modelo, o plano da lente fina é substituído por dois planos, chamados de "planos principais":

• o plano principal “frontal” (ou “primário” ou “lado do objeto”) é usado para medir distâncias no espaço do objeto
• o plano principal “traseiro” (ou “secundário” ou “lado da imagem”) é usado para medir distâncias no espaço da imagem

Estes são planos conjugados com ampliação unitária. Na figura abaixo ( fonte ), são os planos verticais que passam por H ₁ , N ₁ e H ₂ , N ₂ :

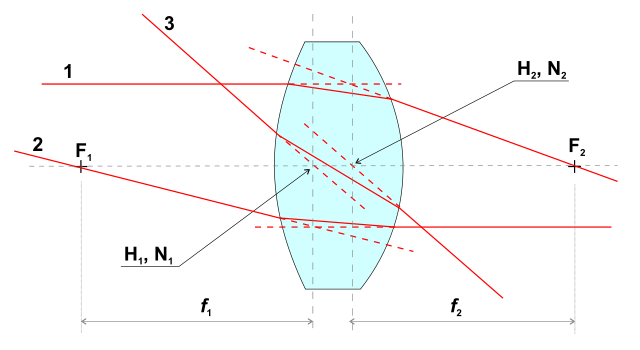
Observe que esta maneira de descrever um sistema óptico em termos de seus pontos cardeais (os itens F _i , H _i e N _i acima) também é aplicável às lentes compostas. Veja, por exemplo, este desenho antigo de uma lente telefoto ( fonte ) em que os dois planos principais (os planos verticais através de N _i e N _o ) estão no lado esquerdo do elemento mais à esquerda:

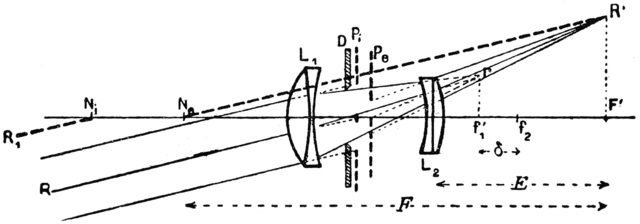
Portanto, sua fórmula ainda é válida, desde que você defina:

• d _o como a distância do sujeito ao plano principal principal
• d _i como a distância do plano principal secundário à imagem

Isso fornece a distância do objeto à imagem como

d _o + e + d _i = 4f + e

na ampliação unitária, onde e é a distância (possivelmente negativa) entre os planos principais. Observe que a aproximação da lente fina diz essencialmente que os planos principais são coincidentes (e = 0), mas não é aplicável ao seu caso.

Para mais informações sobre este tópico, você pode dar uma olhada em:

• este pequeno vídeo sobre aviões principais
• estas notas de aula sobre lentes grossas

O equívoco da lente fina

Eu escrevi essa resposta principalmente para ajudar a esclarecer um equívoco popular, que aparece em algumas das respostas aqui, incluindo a que você aceitou: que uma lente fotográfica é equivalente a uma lente fina.

Acontece que na maioria das situações fotográficas (basicamente todas as situações não macro), a distância do objeto à lente é muito maior do que qualquer distância característica da própria lente. Nessas situações, não importa realmente qual ponto de referência você usa para medir a distância do objeto. É conveniente esquecer a distância que separa os planos principais e considerar que o plano principal traseiro é o único que importa. Isso é equivalente à configuração e = 0, que é basicamente a aproximação da lente fina.

A adesão a essa aproximação torna o aprendizado da ótica muito mais simples, pois você não precisa entender noções como planos principais, pontos principais ou nodais, espaço de objeto, espaço de imagem e assim por diante. Considerando que:

• a aproximação é boa o suficiente para a maioria dos propósitos (não macro)
• o conhecimento em óptica é útil apenas para um fotógrafo em nível qualitativo, pois você não vai projetar lentes e não precisa de conhecimentos em óptica para se tornar um ótimo fotógrafo.

é compreensível que a lente fina seja o modelo mais comumente ensinado aos fotógrafos. E, no entanto, a aproximação é interrompida ao lidar com uma lente espessa e complexa a distâncias macro. As respostas que informam que a distância focal é um quarto da distância entre o objeto e a imagem ilustram como esse equívoco leva as pessoas a postar respostas erradas.

A distância de trabalho é medida da frente da lente ao objeto. Para sua lente Macro EF 100mm f / 2.8 L IS USM, a distância de trabalho na distância mínima de foco (MFD) / ampliação total é de aproximadamente 133mm.

A distância do foco é medida do sujeito ao plano de imagem (filme ou sensor). Para sua lente Macro EF 100mm f / 2.8 L IS USM, a distância do foco na ampliação total / MFD é de 300mm.

As distâncias focais da maioria das lentes são medidas quando a lente é focada no infinito (e depois arredondada para a distância focal "padrão" mais próxima). À medida que a distância do foco é reduzida, o ângulo de visão fornecido pela lente muda frequentemente. Isto é o que é conhecido como foco de respiração . O MFD de 300 mm da sua macro EF 100 mm f / 2.8 L IS USM nos revela que a distância focal efetiva na ampliação de 1: 1 é de cerca de 75 mm. Isso é bastante comum para uma lente Macro com distância focal na faixa de 90 a 105 mm. A Macro Tamron 90mm f / 2.8 Di VC USD (F017), por exemplo, também possui um MFD de 300mm com ampliação de 1: 1.

Além disso, a distância focal para uma lente composta é aproximada da distância focal que uma única lente precisaria para fornecer a mesma quantidade de ampliação. Uma lente composta é um sistema de várias lentes, geralmente dispostas em grupos, que juntas atuam como uma única lente. Praticamente todas as lentes disponíveis comercialmente para sistemas de câmeras com lentes intercambiáveis ​​são lentes compostas. A sua EF 100mm f / 2.8 L IS Macro possui 15 elementos de lente organizados em 12 grupos.

Para a maioria das lentes grande angular que possuem um design de retrofoco, esse ponto teórico simples de lente única está bem atrás da parte frontal da lente. Para lentes telefoto, este ponto é, por definição, na frente da frente da lente.

Quando focada na distância mínima de foco de 300 mm (MFD), a parte frontal da sua macro EF 100 mm f / 2.8 L IS USM fica a cerca de 168 mm na frente do sensor. Mas o campo de visão e ampliação fornecido pela lente no MFD torna efetivamente uma lente de 75 mm nessa distância de foco. Isso significa que uma lente simples de 75 mm precisa estar a 150 mm na frente do sensor (que também a coloca a 150 mm de distância do objeto) para ampliação de 1: 1. Isso coloca o ponto central efetivo da sua EF 100mm f / 2.8 Macro cerca de 18mm atrás da frente da lente quando focado no MFD.

Então, acho que estou perdendo alguma coisa, alguém pode explicar onde estou errado?

Ao aplicar fórmulas como as da sua pergunta, é necessário usar 75 mm para a distância focal da lente quando ela estiver focada no MFD.