Talvez o próprio algoritmo não seja tão obscuro, mas quem pode nomear uma implementação que é realmente usada na prática? Eu posso!
O TIGCC (um compilador baseado em GCC para calculadoras gráficas TI-89/92 / V200) usa a classificação Shell para a qsortimplementação em sua biblioteca padrão:
__ATTR_LIB_C__ void qsort(void *list, short num_items, short size, compare_t cmp_func)
{
unsigned short gap,byte_gap,i,j;
char *p,*a,*b,temp;
for (gap=((unsigned short)num_items)>>1; gap>0; gap>>=1) // Yes, this is not a quicksort,
{ // but works fast enough...
byte_gap=gap*(unsigned short)size;
for(i=byte_gap; i<((unsigned short)num_items)*(unsigned short)size; i+=size)
for(p=(char*)list+i-byte_gap; p>=(char*)list; p-= byte_gap)
{
a=p; b=p+byte_gap;
if(cmp_func(a,b)<=0) break;
for(j=size;j;j--)
temp=*a, *a++=*b, *b++=temp;
}
}
}
A classificação do shell foi escolhida em favor do quicksort para manter o tamanho do código baixo. Embora sua complexidade assintótica seja pior, a TI-89 não possui muita RAM (190K, menos o tamanho do programa e o tamanho total de qualquer variável não arquivada), portanto, é um pouco seguro assumir que o número de itens será abaixo.
Uma implementação mais rápida foi escrita depois que eu reclamei sobre ser muito lenta em um programa que eu estava escrevendo. Ele usa melhores tamanhos de espaço, além de otimizações de montagem. Pode ser encontrado aqui: qsort.c
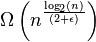 de execução para ϵ > 0.
de execução para ϵ > 0.