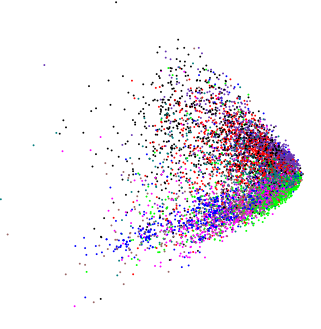
Supondo que as variáveis sejam positivas ou não negativas, as bordas da borda são apenas pontos além dos quais os dados se tornariam 0 ou negativos, respectivamente. Como esses dados da vida real tendem a ser distorcidos corretamente, vemos maior densidade de pontos na extremidade inferior de sua distribuição e, portanto, maior densidade no "ponto" da cunha.
De um modo mais geral, o PCA é simplesmente uma rotação dos dados e as restrições nesses dados geralmente serão visíveis nos componentes principais da mesma maneira mostrada na pergunta.
Aqui está um exemplo usando várias variáveis log-normalmente distribuídas:
library("vegan")
set.seed(1)
df <- data.frame(matrix(rlnorm(5*10000), ncol = 5))
plot(rda(df), display = "sites")

Dependendo da rotação implícita nos dois primeiros PCs, você poderá ver a cunha ou uma versão um pouco diferente, mostrada aqui em 3d usando ( ordirgl()no lugar de plot())

Aqui, em 3d, vemos vários picos saindo da massa central.
XEu∼ ( N) ( μ = 0 , σ= 1 )
set.seed(1)
df2 <- data.frame(matrix(rnorm(5*10000), ncol = 5))
plot(rda(df2), display = "sites")


E para variáveis aleatórias positivas uniformes, vemos um cubo
set.seed(1)
df3 <- data.frame(matrix(runif(3*10000), ncol = 3))
plot(rda(df3), display = "sites")


Observe que aqui, para ilustração, mostro o uniforme usando apenas 3 variáveis aleatórias, portanto, os pontos descrevem um cubo em 3d. Com dimensões mais altas / mais variáveis, não podemos representar perfeitamente o hipercubo 5d em 3d e, portanto, a forma distinta de "cubo" fica distorcida. Problemas semelhantes afetam os outros exemplos mostrados, mas ainda é fácil ver as restrições nesses exemplos.
Para seus dados, uma transformação de log das variáveis anteriores ao PCA puxaria as caudas e esticaria os dados agrupados, assim como você pode usar essa transformação em uma regressão linear.
Outras formas podem surgir em gráficos de PCA; uma dessas formas é um artefato da representação métrica preservada no PCA e é conhecida como ferradura . Para dados com um gradiente longo ou dominante (as amostras organizadas em uma única dimensão com variáveis aumentando de 0 a um máximo e depois diminuindo novamente a 0 ao longo de partes dos dados são conhecidas por gerar esses artefatos.
ll <- data.frame(Species1 = c(1,2,4,7,8,7,4,2,1,rep(0,10)),
Species2 = c(rep(0, 5),1,2,4,7,8,7,4,2,1, rep(0, 5)),
Species3 = c(rep(0, 10),1,2,4,7,8,7,4,2,1))
rownames(ll) <- paste0("site", seq_len(NROW(ll)))
matplot(ll, type = "o", col = 1:3, pch = 21:23, bg = 1:3,
ylab = "Abundance", xlab = "Sites")

que produz uma ferradura extrema, onde pontos nas extremidades dos eixos se dobram de volta para o meio.

 .
. (exceto neste caso, eu realmente queria saber se existe alguma estrutura interna).
(exceto neste caso, eu realmente queria saber se existe alguma estrutura interna).






