Explicação passo a passo da validação cruzada com dobras K com pesquisa em grade para otimizar hiperparâmetros

Estou ciente das vantagens da validação cruzada k-fold (e deixe-o-fora), bem como das vantagens de dividir seu conjunto de treinamento para criar um terceiro conjunto de 'validação', que você usa para avaliar modele o desempenho com base nas opções de hiperparâmetros, para que você possa otimizar e ajustá-los e escolher os melhores para finalmente serem avaliados no conjunto de testes real. Eu implementei esses dois independentemente em vários conjuntos de dados.

No entanto, não sei exatamente como integrar esses dois processos. Eu certamente estou ciente de que isso pode ser feito (validação cruzada aninhada, eu acho?), E já vi pessoas explicando isso, mas nunca com detalhes suficientes para entender realmente os detalhes do processo.

Existem páginas com gráficos interessantes que fazem alusão a esse processo (como este ), sem ser claro sobre a execução exata das divisões e loops. Aqui, o quarto é claramente o que eu quero fazer, mas o processo não é claro:

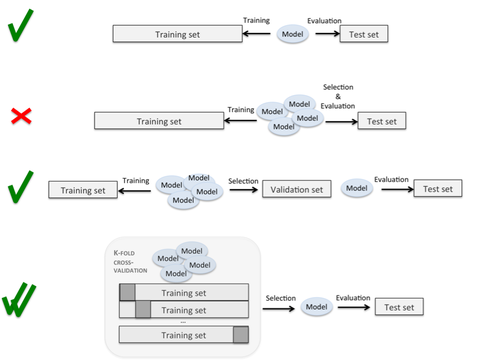
Existem perguntas anteriores neste site, mas, embora elas descrevam a importância de separar conjuntos de validação de conjuntos de testes, nenhum deles especifica o procedimento exato pelo qual isso deve ser feito.

É algo como: para cada uma das k dobras, trate essa dobra como um conjunto de teste, trate uma dobra diferente como um conjunto de validação e treine o resto? Parece que você teria que repetir todo o conjunto de dados k * k vezes, para que cada dobra seja usada como treinamento, teste e validação pelo menos uma vez. A validação cruzada aninhada parece implicar que você faça uma divisão de teste / validação dentro de cada uma das suas k dobras, mas certamente esses dados não podem ser suficientes para permitir o ajuste eficaz dos parâmetros, especialmente quando k é alto.

Alguém poderia me ajudar, fornecendo uma explicação detalhada dos loops e divisões que permitem a validação cruzada dobra em k (de modo que você possa eventualmente tratar todos os pontos de dados como um caso de teste) enquanto executa o ajuste de parâmetros (para que você não pré-especifique parâmetros do modelo e, em vez disso, escolha aqueles que apresentam melhor desempenho em um conjunto de validação separado)?

Aqui está o procedimento de validação cruzada aninhada "padrão" para comparar entre um conjunto fixo de modelos (por exemplo, pesquisa em grade):

• Divida aleatoriamente o conjunto de dados em dobras.$K$
• Para de 1 a : $i$$K$
  • Seja testdobra .$i$
  • Vamos trainvalser todos os dados, exceto o que é em test.
  • Divida aleatoriamente trainvalem subpastas . Portanto, cada subpasta possui alguns elementos da dobra externa 1, alguns da dobra externa 2, ..., mas nenhum deles possui nenhum da dobra externa .$L$$(i, 1), (i, 2), \dots, (i, L)$$(i, j)$$i$
  • Para de 1 a : $j$$L$
    • Seja valdobrado .$(i, j)$
    • Let trainSer todos os dados que não estão em um testou val.
    • Treine cada parâmetro proposto configurado traine avalie-o val, mantendo o controle da precisão da classificação, RMSE, qualquer que seja o critério que você deseja usar.
  • Observe a pontuação média de cada conjunto de parâmetros sobre as dobras em e escolha a melhor.$L$
  • Treine um modelo com esse melhor conjunto de parâmetros trainval.
  • Avalie teste salve a precisão / RMSE / o que for.
• Relate a média / média + std / boxplot / qualquer uma das precisão$K$

A primeira etapa é dividir o conjunto de dados inteiro em conjunto de treinamento e conjunto de testes. E então, para o conjunto de treinamento, você pode aplicar a validação cruzada k-fold. Cada vez que você usa a dobra k-1 para treinar o modelo e usa outra dobra como conjunto de validação para avaliar o desempenho do modelo. Nesta etapa, você pode obter um modelo com melhor desempenho no conjunto de treinamento. Por fim, você pode aplicar esse modelo ao conjunto de testes para avaliar o desempenho do modelo ajustado na segunda etapa. Aqui está um link que você pode achar útil para entender a diferença entre o conjunto de validação e o conjunto de testes. Qual é a diferença entre o conjunto de testes e o conjunto de validação?

De acordo com a resposta de Dougal, você pode conferir o artigo de D. Krstajic et al. "Armadilhas de validação cruzada ao selecionar e avaliar modelos de regressão e classificação", 2014 (doi: 10.1186 / 1758-2946-6-10 https://www.researchgate.net/publication/261217711_Cross-validation_pitfalls_when_selecting_and_assessing_regression_and_classification_models) Lá, eles usam validação cruzada aninhada para avaliação de modelo e validação cruzada de pesquisa em grade para selecionar os melhores recursos e hiperparâmetros a serem empregados no modelo final selecionado. Basicamente, eles apresentam algoritmos diferentes para aplicar a validação cruzada com repetições e também usando a técnica aninhada, que visa fornecer melhores estimativas de erro. No final, eles elaboram os experimentos realizados empregando os diferentes algoritmos para avaliação e seleção de modelos. Conforme mencionado pelos autores na seção Discussão do artigo: "Até onde sabemos, a validação cruzada aninhada é a melhor abordagem não paramétrica para avaliação de modelo quando a validação cruzada é usada para seleção de modelo".