O que é o teorema de Bayes?

Quais são as principais idéias, isto é, conceitos relacionados ao teorema de Bayes ? Não estou pedindo nenhuma derivação de notação matemática complexa.

O teorema de Bayes é um resultado relativamente simples, mas fundamental, da teoria das probabilidades que permite o cálculo de certas probabilidades condicionais. Probabilidades condicionais são apenas aquelas probabilidades que refletem a influência de um evento na probabilidade de outro.

Simplificando, em sua forma mais famosa, ele afirma que a probabilidade de uma hipótese com dados novos ( P (H | D) ; chamada de probabilidade posterior) é igual à seguinte equação: a probabilidade dos dados observados com base na hipótese ( P (D | H) ; chamada de probabilidade condicional), vezes a probabilidade da teoria ser verdadeira antes de novas evidências ( P (H) ; chamada de probabilidade anterior de H), dividida pela probabilidade de ver esses dados, período ( P (D ); chamada de probabilidade marginal de D).

Formalmente, a equação fica assim:

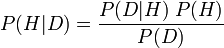
A importância do teorema de Bayes se deve em grande parte ao fato de seu uso adequado ser um ponto de discórdia entre as escolas de pensamento sobre probabilidade. Para um bayesiano subjetivo (que interpreta a probabilidade como sendo graus subjetivos de crença), o teorema de Bayes fornece a pedra angular para testes de teoria, seleção de teoria e outras práticas, inserindo seus julgamentos de probabilidade subjetiva na equação e seguindo com ela. Para um frequentista (que interpreta a probabilidade como limitando as frequências relativas ), esse uso do teorema de Bayes é um abuso, e eles se esforçam para, em vez disso, usar priors significativos (não subjetivos) (como fazem os bayesianos objetivos sob outra interpretação da probabilidade).

Sinto muito, mas parece haver alguma confusão aqui: o teorema de Bayes não está em discussão sobre o interminável debate bayesiano- freqüentista . É um teorema que é consistente com as duas escolas de pensamento (dado que é consistente com os axiomas de probabilidade de Kolmogorov).

Certamente, o teorema de Bayes é o núcleo da estatística bayesiana, mas o próprio teorema é universal. O conflito entre frequentistas e bayesianos refere-se principalmente a como as distribuições anteriores podem ser definidas ou não.

Portanto, se a pergunta é sobre o teorema de Bayes (e não as estatísticas bayesianas):

O teorema de Bayes define como se pode calcular probabilidades condicionais específicas. Imagine, por exemplo, que você saiba: a probabilidade de alguém ter o sintoma A, dado que ele tem a doença X p (A | X); a probabilidade de alguém em geral ter a doença X p (X); a probabilidade de alguém em geral ter o sintoma A p (A). com essas três informações, é possível calcular a probabilidade de alguém ter a doença X, uma vez que eles têm o sintoma A p (X | A).

O teorema de Bayes é uma maneira de girar uma probabilidade condicional para outra probabilidade condicional P ( B | A ) .$P(A|B)$$P(B|A)$

Um obstáculo para alguns é o significado de . Essa é uma maneira de reduzir o espaço de eventos possíveis considerando apenas os eventos em que A definitivamente acontece (ou é verdade). Assim, por exemplo, a probabilidade de um dado arremessado acertar mostrando seis, P ( dado aterrissa seis ) é 1/6, no entanto, a probabilidade de um dado acertar seis, desde que tenha um número par, P ( dado pousa seis | dados cai mesmo ) , é 1/3.$P(B|A)$$A$$P(\mbox{dice lands six})$$P(\mbox{dice lands six}|\mbox{dice lands even})$

Você pode derivar o teorema de Bayes da seguinte maneira. Comece com a definição de razão de uma probabilidade condicional:

$P(B|A) = \frac{P(AB)}{P(A)}$

$P(AB)$$A$$B$$P(A)$$A$

$P(A|B)$

$P(A|B) = \frac{P(BA)}{P(B)}$

$P(AB) = P(BA)$$AB = BA$

$P(A|B) = \frac{P(AB)}{P(B)}$

$P(B|A)$$P(AB)$

$P(AB) = P(A|B)P(B)$

e ei presto:

$P(B|A) = \frac{P(A|B)P(B)}{P(A)}$

Quanto ao objetivo de rotacionar uma probabilidade condicional dessa maneira, considere o exemplo comum de tentar inferir a probabilidade de alguém ter uma doença, uma vez que ela tem um sintoma, ou seja, sabemos que ela tem um sintoma - podemos apenas veja - mas não podemos ter certeza se eles têm ou não uma doença. Vou começar com a fórmula e voltar ao trabalho.

$P(\mbox{disease}|\mbox{symptom}) = \frac{P(\mbox{symptom}|\mbox{disease})P(\mbox{disease})}{P(\mbox{symptom})}$

Portanto, para resolver isso, você precisa conhecer a probabilidade anterior do sintoma, a probabilidade anterior da doença (ou seja, quão comum ou raro são os sintomas e a doença) e também a probabilidade de que alguém tenha um sintoma, pois sabemos que alguém tem. uma doença (por exemplo, através de testes laboratoriais caros e demorados).

Pode ficar muito mais complicado que isso, por exemplo, se você tiver várias doenças e sintomas, mas a idéia é a mesma. De maneira ainda mais geral, o teorema de Bayes geralmente aparece se você tem uma teoria das probabilidades de relações entre causas (por exemplo, doenças) e efeitos (por exemplo, sintomas) e precisa raciocinar para trás (por exemplo, vê alguns sintomas dos quais deseja inferir a doença subjacente).

Existem duas principais escolas de pensamento: Estatística: Frequentista e Bayesiana .

O teorema de Bayes tem a ver com o último e pode ser visto como uma maneira de entender como a probabilidade de uma teoria ser verdadeira é afetada por uma nova evidência. Isso é conhecido como probabilidade condicional. Você pode querer olhar para isso para entender a matemática.

Deixe-me dar uma visão muito, muito intuitiva. Suponha que você esteja jogando uma moeda 10 vezes e receba 8 caras e 2 caudas. A pergunta que vem à sua mente é se essa moeda é tendenciosa ou não.

Agora, se você seguir as definições convencionais ou a abordagem freqüente da probabilidade, poderá dizer que a moeda é imparcial e isso é uma ocorrência excepcional. Portanto, você concluiria que a possibilidade de conseguir um lançamento seguinte também é de 50%.

Mas suponha que você seja bayesiano. Você pensaria que, desde que você tenha um número excepcionalmente alto de cabeças, a moeda tem um viés em direção ao lado da cabeça. Existem métodos para calcular esse possível viés. Você os calcularia e, quando jogar a moeda da próxima vez, definitivamente chamaria de cara.

Portanto, a probabilidade bayesiana é sobre a crença que você desenvolve com base nos dados que observa. Espero que tenha sido bastante simples.

O teorema de Bayes relaciona duas idéias: probabilidade e probabilidade. A probabilidade diz: dado este modelo, estes são os resultados. Então: dada uma moeda justa, recebo cara 50% do tempo. A probabilidade diz: dados esses resultados, é o que podemos dizer sobre o modelo. Então: se você jogar uma moeda 100 vezes e receber 88 cabeças (para pegar no exemplo anterior e torná-lo mais extremo), a probabilidade de o modelo de moeda justo estar correto não é tão alta.

Um dos exemplos padrão usados ​​para ilustrar o teorema de Bayes é a idéia de testar uma doença: se você fizer um teste com uma precisão de 95% para uma doença que 1 em 10000 da população tem e se testar positivo, quais são as chances que você tem a doença?

A resposta ingênua é de 95%, mas isso ignora a questão de que 5% dos testes em 9999 em 10.000 pessoas darão um falso positivo. Portanto, suas chances de ter a doença são muito inferiores a 95%.

Meu uso da vaga frase "quais são as chances" é deliberado. Para usar a linguagem de probabilidade / probabilidade: a probabilidade de que o teste seja preciso é de 95%, mas o que você deseja saber é a probabilidade de ter a doença.

Um pouco superficial: O outro exemplo clássico que o teorema de Bayes é usado para resolver em todos os livros didáticos é o problema de Monty Hall: você está em um programa de perguntas e respostas. Há um prêmio atrás de uma das três portas. Você escolhe a porta um. O anfitrião abre a porta três para não revelar nenhum prêmio. Você deve mudar para a porta dois, se tiver a chance?

Gosto da reformulação da pergunta (cortesia da referência abaixo): você está em um programa de perguntas e respostas. Há um prêmio atrás de uma de um milhão de portas. Você escolhe a porta um. O host abre todas as outras portas, exceto a porta 104632, para não revelar nenhum prêmio. Você deve mudar para a porta 104632?

Meu livro favorito que discute o teorema de Bayes, muito da perspectiva bayesiana, é "Teoria da informação, inferência e algoritmos de aprendizagem", de David JC MacKay. É um livro da Cambridge University Press, ISBN-13: 9780521642989. Minha resposta é (espero) uma destilação do tipo de discussão feita no livro. (Aplicam-se regras usuais: não tenho afiliações com o autor, apenas gosto do livro).

O teorema de Bayes, na sua forma mais óbvia, é simplesmente uma afirmação de duas coisas:

1. $P(HD|I)=P(DH|I)$
2. $P(HD|I)=P(H|I)P(D|HI)$

Então, usando a simetria:

$P(D|I) \neq 0$$P(D|I)$

Então é isso? Como algo tão simples pode ser tão incrível? Como na maioria das coisas, "é a jornada mais importante que o destino". O teorema de Bayes oscila por causa dos argumentos que o levam.

$P(H|I)=1-P(\overline{H}|I)$

Agora, a "regra" na lógica dedutiva é que, se você tem um relacionamento "A implica B", também tem "Não B implica Não A". Portanto, temos "um raciocínio consistente implica no teorema de Bayes". Isso significa "O teorema de não Bayes implica em raciocínio não consistente". ou seja, se o seu resultado não for equivalente a um resultado bayesiano por algum motivo e probabilidade anteriores, você estará raciocinando inconsistentemente.

Esse resultado é chamado de teorema de Cox e foi provado em "Álgebra de provável inferência" na década de 1940. Uma derivação mais recente é dada na teoria da Proabilidade: A lógica da ciência.

Eu realmente gosto da introdução de Kevin Murphy ao Teorema de Bayes http://www.cs.ubc.ca/~murphyk/Bayes/bayesrule.html

A citação aqui é de um artigo de economista:

http://www.cs.ubc.ca/~murphyk/Bayes/economist.html

A essência da abordagem bayesiana é fornecer uma regra matemática que explique como você deve mudar suas crenças existentes à luz de novas evidências. Em outras palavras, permite que os cientistas combinem novos dados com seus conhecimentos ou experiência existentes. O exemplo canônico é imaginar que um recém-nascido precoce observa seu primeiro pôr do sol e se pergunta se o sol nascerá novamente ou não. Ele atribui probabilidades anteriores iguais a ambos os resultados possíveis e representa isso colocando um mármore branco e um mármore preto em uma bolsa. No dia seguinte, quando o sol nasce, a criança coloca outro mármore branco na bolsa. A probabilidade de um mármore arrancado aleatoriamente da bolsa ser branca (ou seja, o grau de crença da criança em futuros nascer do sol) passou de metade para dois terços. Após o nascer do sol no dia seguinte, a criança acrescenta outro mármore branco, e a probabilidade (e, portanto, o grau de crença) vai de dois terços a três quartos. E assim por diante. Gradualmente, a crença inicial de que o sol tem a mesma probabilidade de não nascer todas as manhãs é modificada para se tornar quase certa de que o sol sempre nascerá.