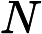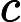Deveríamos considerar uma lei da natureza?

Muitos especialistas acreditam que a conjectura é verdadeira e a usa em seus resultados. Minha preocupação é que a complexidade dependa fortemente da conjectura .P ≠ N $\mathsf{P} \neq \mathsf{NP}$$\mathsf{P} \neq \mathsf{NP}$

Então, minha pergunta é:

Desde que a conjectura não seja comprovada, alguém deve / deve considerá-la como uma lei da natureza, conforme indicado na citação de Strassen? Ou devemos tratá-lo como uma conjectura matemática que talvez seja provada ou refutada algum dia?$\mathsf{P}\neq\mathsf{NP}$

Citar:

"A evidência a favor das hipóteses de Cook e Valiant é tão avassaladora, e as conseqüências de seu fracasso são tão grotescas que seu status talvez possa ser comparado ao das leis físicas e não às conjecturas matemáticas comuns".

[Volker Strassen é laudation ao ganhador do Prêmio Nevanlinna, Leslie G. Valar, em 1986]

Eu faço essa pergunta ao ler os resultados da publicação Física no TCS? . Talvez seja interessante notar que a complexidade computacional tem algumas semelhanças com a física (teórica): muitos resultados importantes da complexidade foram provados assumindo , enquanto que nos resultados físicos teóricos são provados assumindo algumas leis físicas$\mathsf{P} \neq \mathsf{NP}$ P ≠ N P E=m c 2 . Nesse sentido, pode ser considerado algo como . Voltar aos resultados de Física em TCS? :$\mathsf{P} \neq \mathsf{NP}$$E = mc^2$

Poderia (parte do) TCS ser um ramo das ciências naturais?

Esclarecimento:

(veja a resposta de Suresh abaixo)

É legítimo dizer que a conjectura na teoria da complexidade é tão fundamental quanto as leis físicas da física teórica (como disse Strassen)?$\mathsf{P}\neq\mathsf{NP}$

A declaração de Strassen precisa ser contextualizada. Este foi um discurso para um público de matemáticos em 1986, época em que muitos matemáticos não tinham uma opinião alta da ciência da computação teórica. A declaração completa é

Para alguns de vocês, pode parecer que as teorias discutidas aqui se apóiam em bases fracas. Eles não. A evidência a favor das hipóteses de Cook e Valiant é tão avassaladora, e as conseqüências de seu fracasso são tão grotescas que seu status talvez possa ser comparado ao das leis físicas e não às conjecturas matemáticas comuns.

Tenho certeza de que Strassen teve conversas com matemáticos puros que disseram algo ao longo das linhas de

"Você está baseando toda a teoria da complexidade em um castelo de cartas. E se P = NP? Então todos os seus teoremas não terão sentido. Por que você não faz um pouco de esforço e prova que P NP, em vez do que continuar construindo uma teoria sobre fundações tão fracas ".$\neq$

Em 2013, quando P NP é um problema do prêmio Clay há uma dúzia de anos, pode parecer difícil acreditar que algum matemático realmente tenha essas atitudes; no entanto, posso garantir pessoalmente que alguns o fizeram.$\neq$

Strassen continua dizendo que não devemos desistir de procurar uma prova de P NP (implicando indiretamente que é de fato uma conjectura matemática):$\neq$

No entanto, uma prova tradicional seria de grande interesse, e me parece que a hipótese de Valiant pode ser mais fácil de confirmar do que a de Cook ...

então talvez eu o rotulei como uma "hipótese de trabalho" em vez de uma "lei física".

Finalmente, note que os matemáticos também usam tais hipóteses de trabalho. Há um grande número de trabalhos de matemática que provam teoremas cujas afirmações correm "Supondo que a hipótese de Riemann seja verdadeira, então ...".

Eu posso ver três maneiras relacionadas de entender a pergunta:

1) Podemos considerar como um princípio fundamental da teoria da complexidade computacional, mesmo antes de podermos provar isso?$NP \ne P$

2) O princípio se estende além de seu estreito significado matemático?$NP \ne P$

3) O princípio pode ser considerado uma lei física.$NP \ne P$

Penso que existem boas razões para responder 'sim' ou 'sim qualificado' para todas essas três perguntas.

Eu não tenho certeza se entendi. Uma lei física (do tipo que você indica) é uma expressão matemática de um modelo (nesse exemplo, a relatividade) que afirma capturar a realidade. Pode-se provar que uma lei física está errada se a matemática subjacente estiver incorreta, mas também pode estar errada se o modelo subjacente mudar (por exemplo, mecânica newtoniana). P vs NP é uma conjectura matemática específica que é verdadeira ou falsa (e pode ser provável ou não)

Para responder à sua pergunta original:

Sim, pelo menos Scott Aaronson acredita que é uma lei da natureza. Ele propôs a seguinte formulação$P \ne NP$

"A suposição de dureza NP ?: Não há meios físicos para resolver problemas completos de NP em tempo polinomial".

Ele deu uma boa palestra na Universidade de Waterloo intitulada Intratabilidade computacional como uma lei da física

$NL\neq PSPACE$$NP\neq coNP$$P\neq NP$

$\phi$$\phi$

Você pode fazer muitos experimentos sobre velocidades e velocidades e obterá evidências esmagadoras para validar as leis de Newton. Obviamente, você verá coisas muito estranhas em experimentos muito particulares, como a velocidade da luz na água em movimento ou alguns eventos astronômicos. Mas suas evidências esmagadoras lhe dirão: Newton está certo e essas leis são o que você precisa

É claro que Newton "não está certo", e Einstein veio atrás dele.

Para P = NP, podemos ver muitos exemplos em que parece P ≠ NP. Mas, em alguns casos particulares, temos coisas estranhas. Se P ≠ NP, há um número infinito de classes entre elas, portanto, devemos encontrar alguns problemas no NP que não estão no P, mas não estão completos no NP. Não conhecemos nenhum deles, e a maioria dos candidatos provou estar em P.

O que você pensa sobre esse problema depende de onde você deseja olhar. Eu não ficaria surpreso se P = NP.