Avaliando modelos de regressão logística

Essa questão surge da minha confusão real sobre como decidir se um modelo logístico é bom o suficiente. Eu tenho modelos que usam o estado dos pares de projetos individuais dois anos após serem formados como uma variável dependente. O resultado é bem-sucedido (1) ou não (0). Eu tenho variáveis independentes medidas no momento da formação dos pares. Meu objetivo é testar se uma variável, que eu imaginei, influenciaria o sucesso dos pares, afeta esse sucesso, controlando outras influências em potencial. Nos modelos, a variável de interesse é significativa.

Os modelos foram estimados usando a glm()função in R. Para avaliar a qualidade dos modelos, eu fiz algumas coisas: glm()fornece o residual deviance, o AICe o BICpor padrão. Além disso, calculei a taxa de erro do modelo e plotei os resíduos binados.

O modelo completo possui um desvio residual menor, AIC e BIC do que os outros modelos que eu estimei (e que estão aninhados no modelo completo), o que me leva a pensar que esse modelo é "melhor" que os outros.
A taxa de erro do modelo é bastante baixa, IMHO (como em Gelman e Hill, 2007, pp.99 ):
error.rate <- mean((predicted>0.5 & y==0) | (predicted<0.5 & y==1)em torno de 20%.

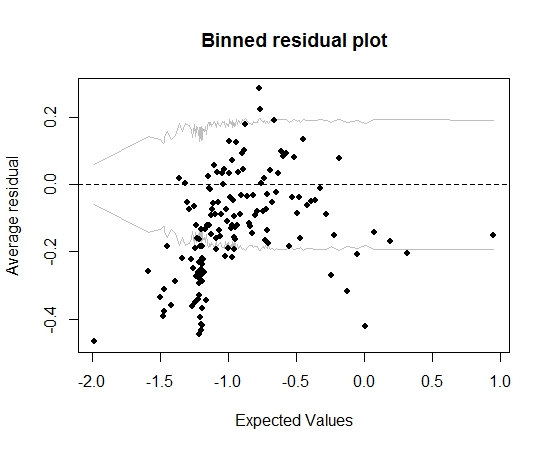
Por enquanto, tudo bem. Porém, quando planto o resíduo acumulado (novamente seguindo o conselho de Gelman e Hill), grande parte das caixas fica fora do IC 95%: Lote de resíduos binados

Esse enredo me leva a pensar que há algo totalmente errado no modelo. Isso deveria me levar a jogar fora o modelo? Devo reconhecer que o modelo é imperfeito, mas mantê-lo e interpretar o efeito da variável de interesse? Eu brinquei com a exclusão de variáveis, por sua vez, e também com algumas transformações, sem realmente melhorar o gráfico de resíduos binados.

Editar:

No momento, o modelo possui uma dúzia de preditores e 5 efeitos de interação.
Os pares são "relativamente" independentes um do outro, no sentido de que todos são formados durante um curto período de tempo (mas não estritamente falando, todos simultaneamente) e há muitos projetos (13k) e muitos indivíduos (19k ), portanto, uma proporção justa de projetos é unida por apenas um indivíduo (existem cerca de 20.000 pares).

r logistic goodness-of-fit residuals

— Antoine Vernet
fonte

Y

$Y$

Com base no que você diz, o tamanho da amostra não parece ser um problema, porque eu tenho cerca de 20.000 mil pares (dos quais aproximadamente 20% são bem-sucedidos).

— Antoine Vernet

Respostas:

A precisão da classificação (taxa de erro) é uma regra de pontuação inadequada (otimizada por um modelo falso), arbitrária, descontínua e fácil de manipular. Não é necessário neste contexto.

Você não indicou quantos preditores havia. Em vez de avaliar o ajuste do modelo, ficaria tentado a ajustá-lo. Uma abordagem de compromisso é assumir que as interações não são importantes e permitir que preditores contínuos não sejam lineares usando splines de regressão. Traçar os relacionamentos estimados. O rmspacote em R torna tudo isso relativamente fácil. Veja http://biostat.mc.vanderbilt.edu/rms para mais informações.

Você pode elaborar "pares" e se suas observações são independentes.

— Frank Harrell
fonte

Se entendi corretamente, seu conselho é concentrar-se no gráfico dos resíduos e corrigir esse problema antes de fazer qualquer outra coisa, eventualmente usando splines de regressão, estou correto? Editei a pergunta para indicar quantos preditores existem e que os pares são "relativamente" independentes.

— Antoine Vernet

Olá, @Frank. Por que você diz que a precisão da classificação é um método ruim? Isso ocorre porque é aqui avaliado nos mesmos dados em que o modelo é derivado?

— Peter Flom - Restabelece Monica

χ^{2}

$\chi^2$

c

$c$

Não, quero dizer, permitir que preditores contínuos operem de maneira não linear na escala de chances de log, expandindo-os em vários termos usando splines cúbicos restritos (splines naturais). Em seguida, plote as transformações estimadas para aprender sobre os efeitos parciais de cada preditor.

— precisa

Obrigado pela contribuição, foi realmente útil. Aprofundando-me com os dados, percebi que tinha problemas de colinearidade (mesmo que não tivesse correlações altas aos pares).

— Antoine Vernet

A situação parece um pouco estranha, mas acho que seu enredo pode fornecer uma pista. Parece que pode haver um relacionamento curvilíneo. É permitido usar termos polinomiais e outras transformações de variáveis preditoras (por exemplo, $x^2$ ) na regressão logística, assim como na regressão OLS. Vale a pena tentar.

— Repor a Monica
fonte