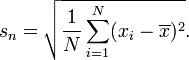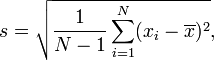Por que as escolas dos EUA e do Reino Unido ensinam diferentes métodos de cálculo do desvio padrão?

15

Pelo que entendi, as escolas do Reino Unido ensinam que o desvio padrão é encontrado usando:

$texto alternativo$

Considerando que as escolas dos EUA ensinam:

$texto alternativo$

(em um nível básico de qualquer maneira).

Isso causou vários problemas aos meus alunos no passado, enquanto eles procuravam na Internet, mas encontraram a explicação errada.

Por que a diferença?

Com conjuntos de dados simples, digamos 10 valores, que grau de erro haverá se o método errado for aplicado (por exemplo, em um exame)?

— Amos
fonte

4

Não tenho certeza se caracterizar uma ou outra como a fórmula "errada" é a maneira de entender o problema. É apenas que o segundo é "melhor" no sentido de que é um estimador imparcial do verdadeiro desvio padrão. Portanto, se você se preocupa com estimativas imparciais, a segunda é 'melhor' / 'correta'.

Eu estava caracterizando a fórmula como "errada" puramente no sentido de que, em um exame, se você usar a fórmula que não é proibida pelo plano de estudos, você terminará com a resposta "errada". Além disso, se os valores não são uma amostra da população em si, certamente a primeira fórmula fornece o valor mais preciso.

— 1933 Amos

14

Srikant, não acho que o segundo seja um estimador imparcial. O quadrado disso é um estimador imparcial da verdadeira variação. No entanto, a desigualdade de Jensen estabelece que a expectativa de uma função curvilínea de uma variável aleatória não é a mesma que a função da expectativa da variável aleatória. Portanto, a segunda fórmula não pode ser um estimador imparcial do verdadeiro desvio padrão.

— Andrew Robinson

Para referência cruzada: também foi solicitado @ m.SE ...

— JM não é estatístico

4

Qualquer escola dos EUA que use o texto elementar muito popular de Freedman, Pisani, & Purves está usando a primeira fórmula (

), portanto, parece incorreto caracterizar isso como uma diferença entre EUA e Reino Unido.

s_{n}

$s_n$

— whuber

18

A primeira fórmula é o desvio padrão da população e a segunda fórmula é o desvio padrão da amostra . A segunda fórmula também está relacionada ao estimador imparcial da variância - consulte a Wikipedia para mais detalhes.

Suponho que (aqui) no Reino Unido eles não fazem a distinção entre amostra e população no ensino médio. Eles certamente não tocam em conceitos como estimadores tendenciosos.

— csgillespie
fonte

4

Colin, um estimador imparcial do desvio padrão não tem uma representação de forma fechada no caso geral. O que existe é o estimador imparcial da variação (s 2 neste caso). Vale ressaltar que ambos são estimadores consistentes da variação da população - e, portanto, pelo teorema do mapeamento contínuo, são os dois estimadores dos desvios padrão. Um ponto relacionado é que s n 2 tem um MSE mais baixo que s 2 . A vantagem adicional de impor imparcialidade é discutível.

— Mornington

@Tirthankar - muito desleixado da minha parte. Eu alterei a resposta um pouco. Obrigado.

— csgillespie

2

Tanto quanto me lembro, fui ensinado o cálculo da 'amostra' em matemática e ciências do GCSE (14 a 16 anos) e a distinção entre populações e amostras e suas medidas de variação associadas foi abordada (embora não em profundidade) no nível A ( 16-18 anos). Portanto, não tenho certeza se essa é uma simples diferença entre Reino Unido / EUA.

— Freya Harrison

11

Como ninguém ainda respondeu à pergunta final - ou seja, para quantificar as diferenças entre as duas fórmulas - vamos cuidar disso.

Por muitas razões, é apropriado comparar os desvios padrão em termos de suas proporções e não em suas diferenças. A proporção é

s_{n} / s = \sqrt{\frac{N - 1}{N}} = \sqrt{1 - \frac{1}{N}} \approx 1 - \frac{1}{2 N} .

$s_n / s = \sqrt{\frac{N-1}{N}} = \sqrt{1 - \frac{1}{N}} \approx 1 - \frac{1}{2N}.$

A aproximação pode ser vista como truncando a série Taylor (alternada) para a raiz quadrada, indicando que o erro não pode exceder $|\binom{1/2}{2}N^{-2}|$ $1 / (8 N^2)$ $N$ $2$

$N$ $5$ $N$ $10$ SDs, como ao comparar os spreads de dois conjuntos de dados. (Quando os conjuntos de dados são equinumerosos, as discrepâncias desaparecem completamente e as duas fórmulas levam a conclusões idênticas.) Provavelmente, essas são as formas de raciocínio que estamos tentando ensinar aos alunos iniciantes; portanto, se os alunos estiverem se preocupando com qual fórmula usar, isso pode ser tomado como um sinal de que o texto ou a classe não está enfatizando o que é realmente importante.

$N$ $t$ $z$ $s$ $s_n$

— whuber
fonte

6

Esta é a correção de Bessel . A versão dos EUA está mostrando a fórmula do desvio padrão da amostra , onde a versão do Reino Unido acima é o desvio padrão da amostra .

— Reed Copsey
fonte

5

Não tenho certeza se isso é puramente uma questão dos EUA vs. Britânica. O restante desta página foi extraído de um FAQ que escrevi ( http://www.graphpad.com/faq/viewfaq.cfm?faq=1383 ).

Como calcular o SD com n-1 no denominador

Calcule o quadrado da diferença entre cada valor e a média da amostra.
Adicione esses valores acima.
Divida a soma por n-1. O resultado é chamado de variação.
Pegue a raiz quadrada para obter o desvio padrão.

Por que n-1?

Por que dividir por n-1 em vez de n ao calcular um desvio padrão? Na etapa 1, você calcula a diferença entre cada valor e a média desses valores. Você não conhece o verdadeiro meio da população; tudo o que você sabe é a média da sua amostra. Exceto nos casos raros em que a média da amostra é igual à média da população, os dados estarão mais próximos da média da amostra do que da média real da população. Portanto, o valor que você calcula na etapa 2 provavelmente será um pouco menor (e não pode ser maior) do que seria se você usasse a verdadeira média da população na etapa 1. Para compensar isso, divida por n-1 em vez de Isso é chamado de correção de Bessel.

Mas por que n-1? Se você soubesse a média da amostra e todos, exceto um dos valores, poderia calcular qual seria esse último valor. Os estatísticos dizem que existem n-1 graus de liberdade.

Quando o SD deve ser calculado com um denominador de n em vez de n-1?

Os livros de estatística geralmente mostram duas equações para calcular o DP, um usando n e outro usando n-1, no denominador. Algumas calculadoras possuem dois botões.

A equação n-1 é usada na situação comum em que você está analisando uma amostra de dados e deseja tirar conclusões mais gerais. O SD calculado dessa maneira (com n-1 no denominador) é o seu melhor palpite para o valor do SD na população geral.

Se você simplesmente deseja quantificar a variação em um determinado conjunto de dados e não planeja extrapolar para tirar conclusões mais amplas, é possível calcular o SD usando n no denominador. O SD resultante é o SD desses valores específicos. Não faz sentido calcular o DP dessa maneira, se você quiser estimar o DP da população a partir da qual esses pontos foram extraídos. Só faz sentido usar n no denominador quando não há amostragem de uma população, não há desejo de tirar conclusões gerais.

O objetivo da ciência é quase sempre generalizar, portanto a equação com n no denominador não deve ser usada. O único exemplo em que consigo pensar em onde pode fazer sentido é quantificar a variação entre as notas dos exames. Mas muito melhor seria mostrar um gráfico de dispersão de cada pontuação ou um histograma de distribuição de frequência.

— Harvey Motulsky
fonte

1

Eu não estava sugerindo isso, estava apenas curioso para saber por que essa diferença poderia ter surgido, que tipo de erro seguir o conselho errado poderia dar e se havia uma explicação decente da diferença que eu poderia dar aos meus alunos. .

— 1937 Amos

@harvey - o link está morto

— baxx

1

@axx .. Obrigado por apontar isso. Fixo.

— Harvey Motulsky 13/01

3

Since N is the number of points in the data set, one could argue that by calculating the mean one has reduced the degree of freedom in the data set by one (since one introduced a dependency into the data set), so one should use N-1 when estimating the standard deviation from a data set for which one had to estimate the mean before.

— Benjamin Bannier
fonte